共通テスト 情報I 対策問題集アプリ 第4問(共通テスト 試作問題-共通テスト 試作問題)

　当サイト・webアプリケーション・ページは、2025 年度大学入学共通テストから新教科として導入された「情報1」 の学習サイトです。
　現役ソフトウェアエンジニアと受験生向け塾講師の両経験を持つ運営主が、問題の作成からアプリの運営・開発まで一貫して行なっています。
　このページは問題一覧です。全ての問題を確認することで、情報1試験のインプット対策ができます。 　$ 問題タイトル：第4問問題カテゴリ：共通テスト 試作問題問題文：次の文章を読み、後の問い（問1～5）に答えよ。 次の表1は、国が実施した生活時間の実態に関する統計調査をもとに、15歳以上19歳以下の若年層について、都道府県別に平日1日の中で各生活行動に費やした時間（分）の平均値を、スマートフォン・パソコンなどの使用時間をもとにグループに分けてまとめたものの一部である。ここでは、1日のスマートフォン・パソコンなどの使用時間が1時間未満の人を表1-A、3時間以上6時間未満の人を表1-Bとしている。 （表1-A、表1-B：生活行動時間に関する都道府県別平均値） 花子さんたちは、表1-Aをスマートフォン・パソコンなどの使用時間が短いグループ、表1-Bをスマートフォン・パソコンなどの使用時間が長いグループと設定し、これらのデータから、スマートフォン・パソコンなどの使用時間と生活行動に費やす時間の関係について分析してみることにした。 ただし、表1-A、表1-Bにおいて一か所でも項目のデータに欠損値がある場合は、それらの都道府県を除外したものを全体として考える。なお、以下において、データの範囲については、外れ値も含めて考えるものとする。解説文：正解は「1」です。 提示された表1-A、表1-Bのデータは、「1日の中で各生活行動に費やした時間の合計」を示したものです。 選択肢1にあるような「朝」や「夜」といった時間帯別の内訳に関するデータは含まれていないため、この仮説は表のデータだけからは分析できません。 正解は「2」です。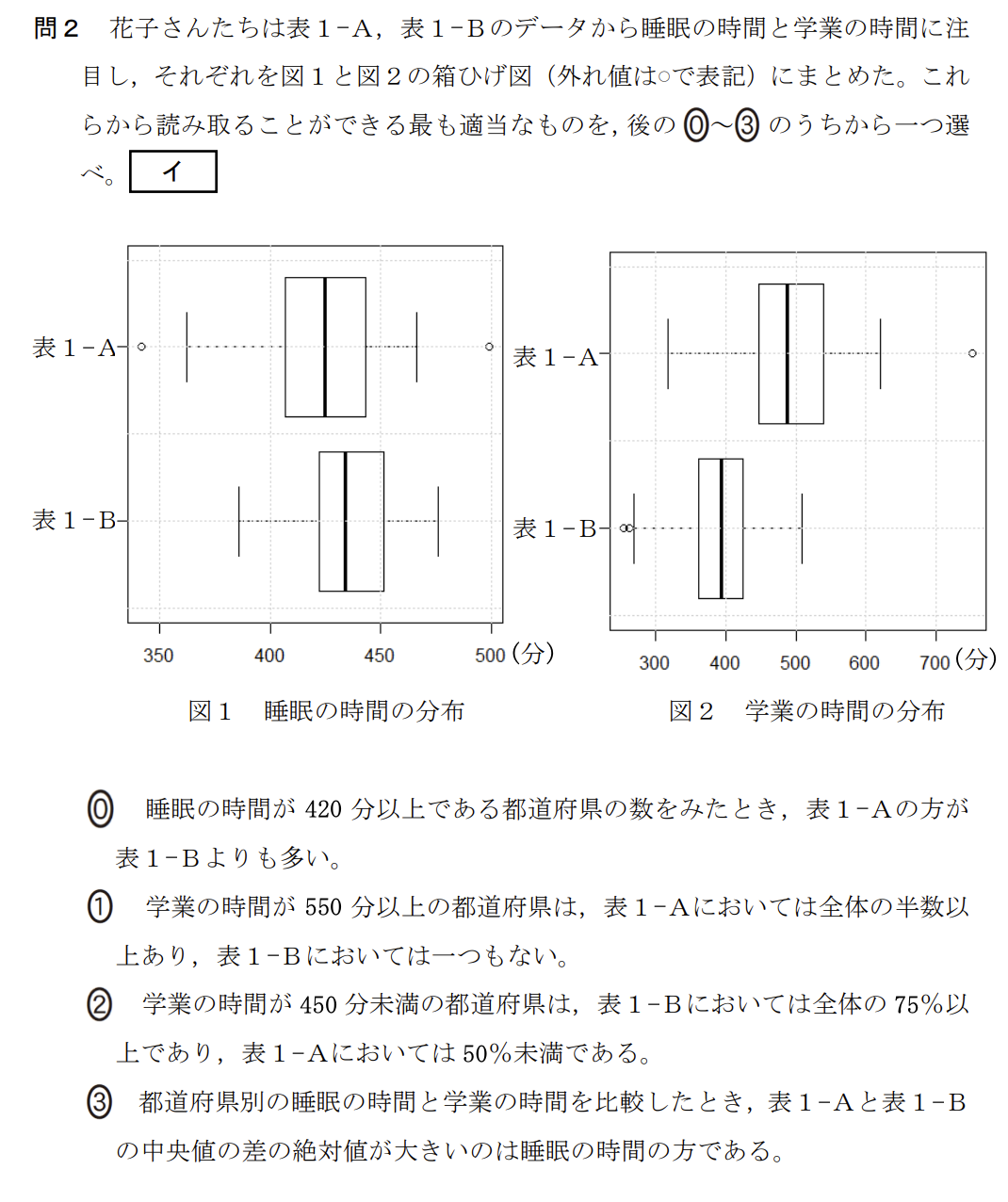 箱ひげ図の読み取り問題です。 ・選択肢2について： 図2（学業の時間）を確認します。 表1-Bの箱ひげ図を見ると、第3四分位数（箱の右端、下から75%の位置）が420分付近にあります。これは、データの75%以上が450分未満であることを示しています。 一方、表1-Aの箱ひげ図では、第2四分位数（中央値、箱の中央の線）が480分付近にあります。これは、データの50%以上が450分以上（つまり450分未満は50%未満）であることを示しています。 したがって、この記述は図から読み取れる内容として正しいです。 正解は「0」です。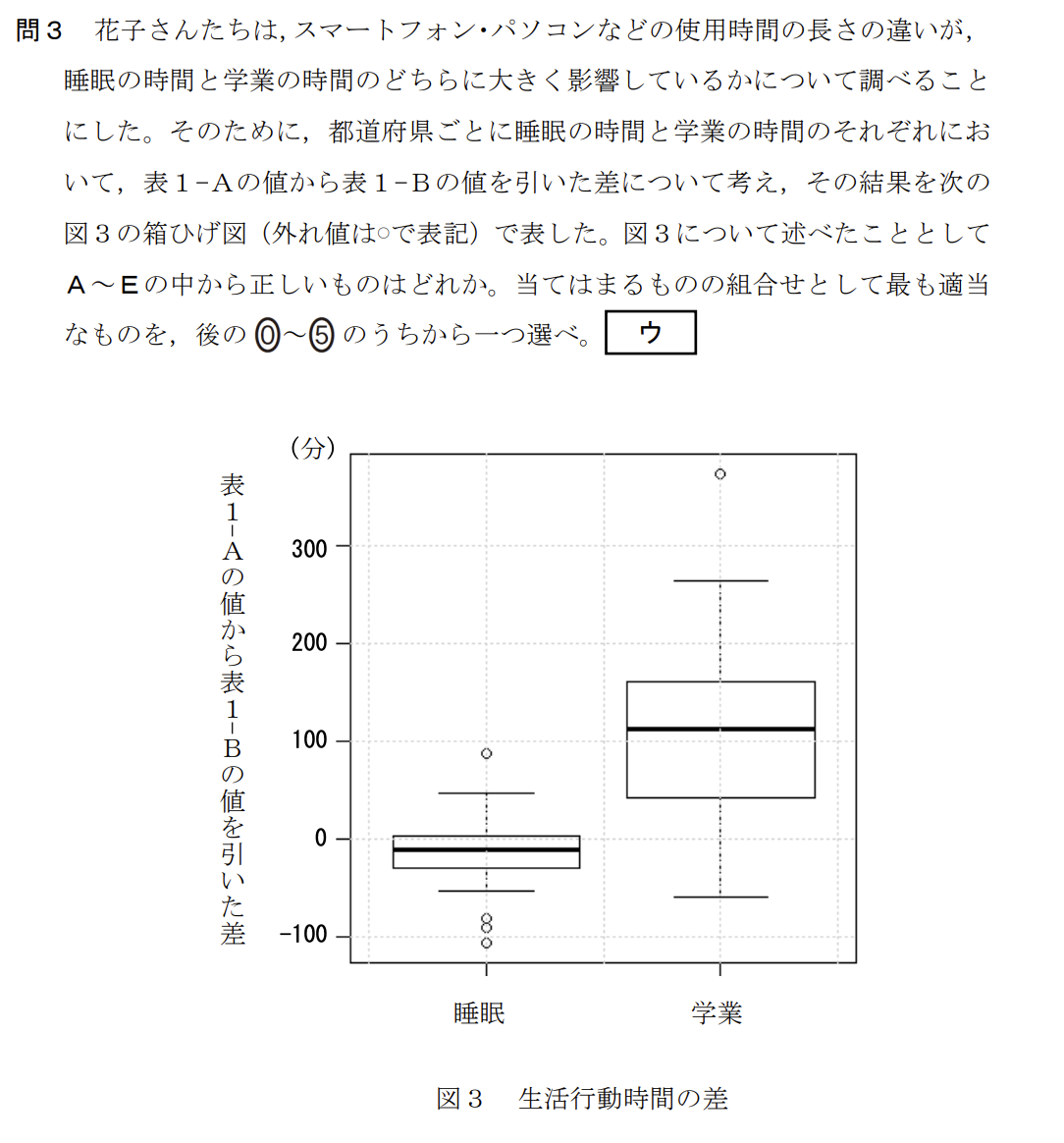 図3は「表1-A（使用時間短）の値から 表1-B（使用時間長）の値を引いた差」を示しています。 ・記述A（学業）：箱ひげ図全体がプラス側（0より上）にあります。これは「1-A - 1-B > 0」、つまり「1-A（短いグループ）の方が学業時間が長い」ことを意味しており、正しいです。 ・記述B（睡眠）：箱ひげ図全体がマイナス側（0より下）にあります。これは「1-A - 1-B < 0」、つまり「1-Aの方が睡眠時間が短い」ことを意味するため、記述Bは誤りです。 ・記述C（比較）：学業の時間の箱ひげ図は、睡眠の時間に比べて0からの距離（絶対値）が大きく、差が顕著です。したがって、記述Cは正しいです。 AとCが正しいため、正解は「0」となります。 正解は「2」です。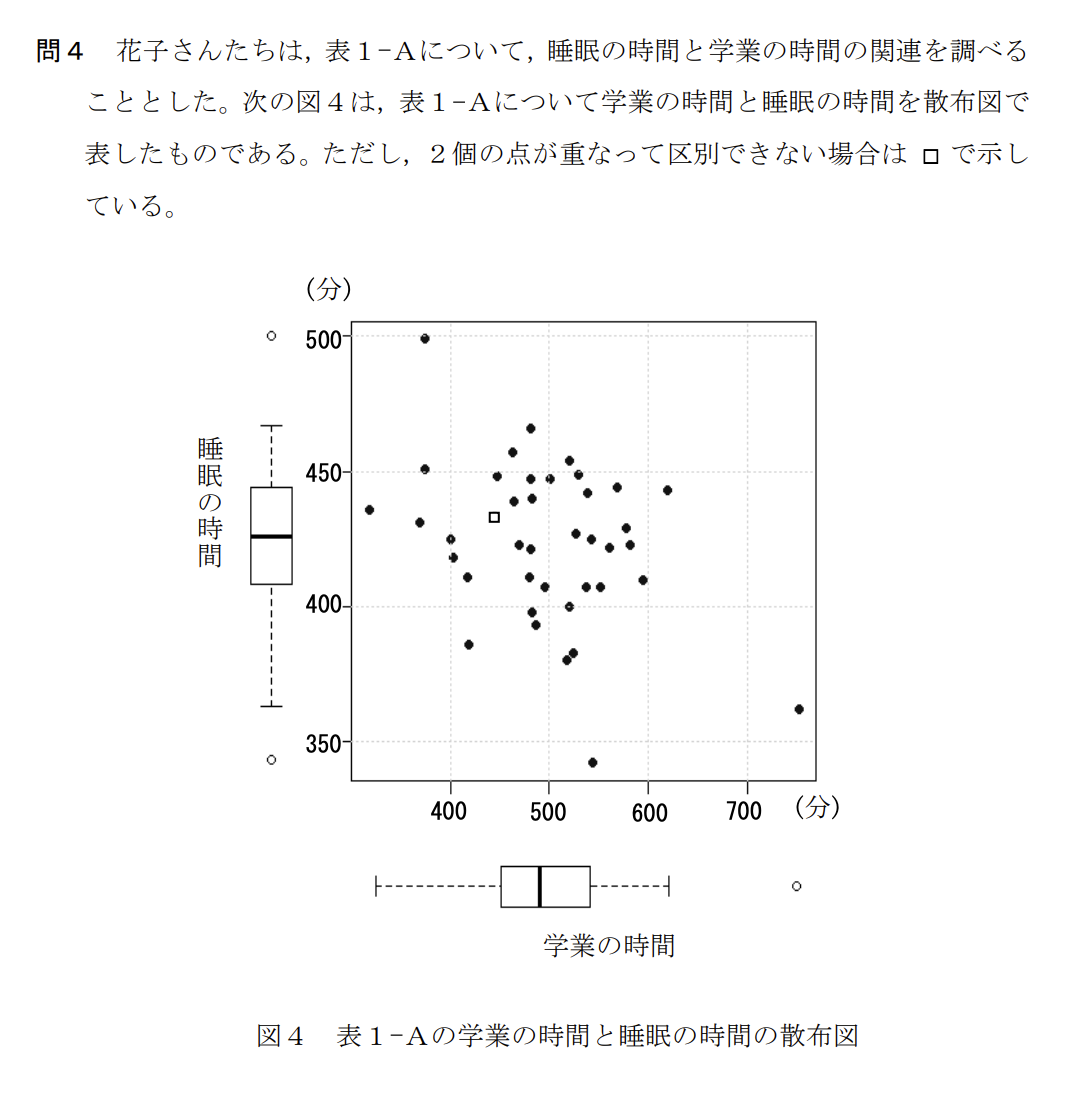 問題文に「弱い負の相関がある」と記述されています。 「負の相関」とは、一方の値が増加すると、もう一方の値が減少する傾向のことです。 したがって、「学業の時間が長い（増加）ほど、睡眠の時間が短くなる（減少）」という記述が最も適当です。 正解は「2」です。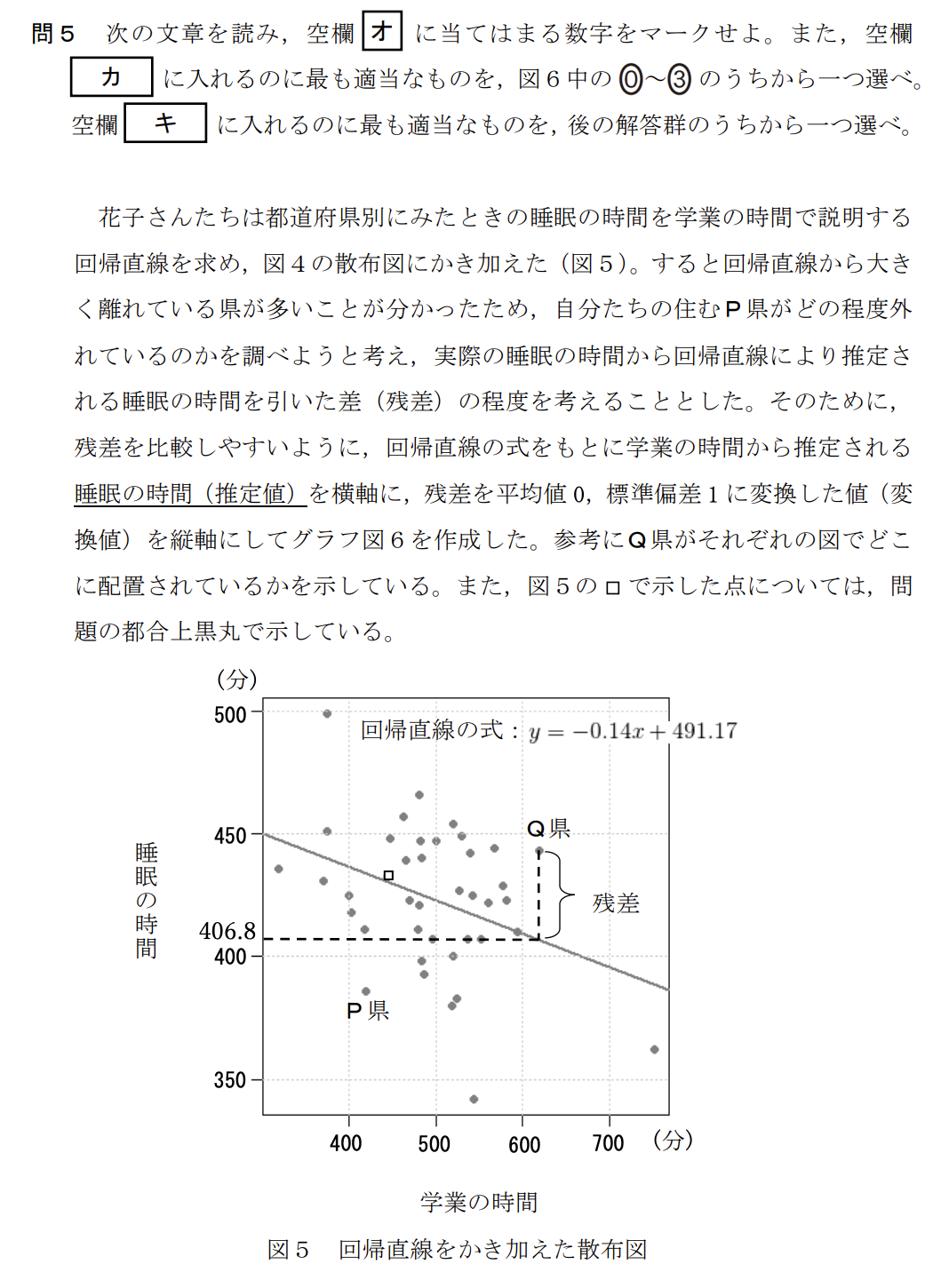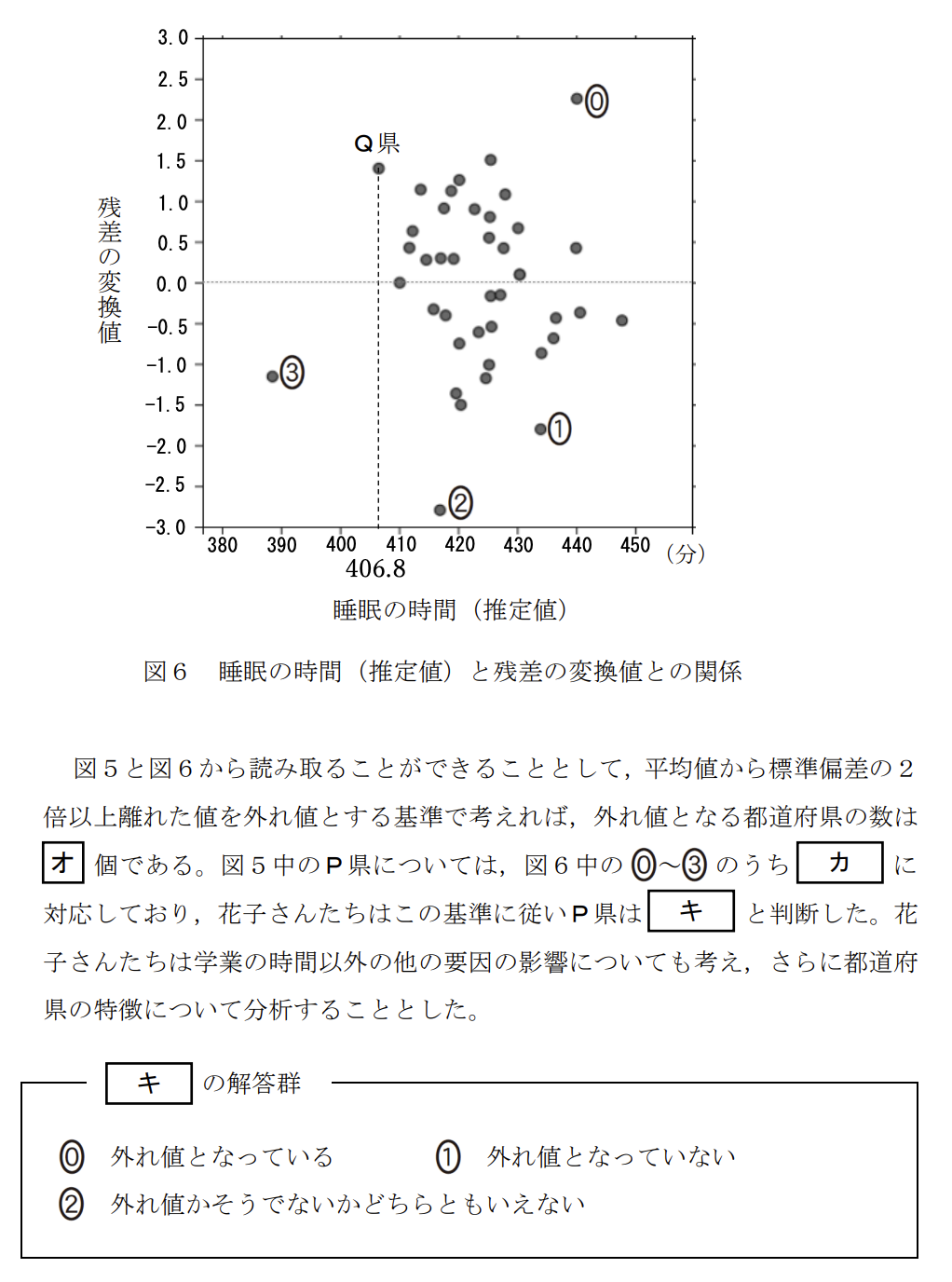 図6は、縦軸が「残差の変換値（標準偏差）」を表しています。 問題文の条件「平均値から標準偏差の2倍以上離れた値を外れ値とする」に従うと、縦軸の値の絶対値が2以上（2.0以上 または -2.0以下）の点が外れ値となります。 図6を確認すると、 ・2.0より上の範囲に1つ（点0） ・-2.0より下の範囲に1つ（点2） 合計で2つの点が存在するため、答えは「2」です。 正解は「1」です。 図5（散布図）において、P県は回帰直線よりも下側に位置しています。 これは、「実際の値 < 推定値」であることを意味し、残差（実際 - 推定）は「負（マイナス）」になります。 また、P県の横軸（学業の時間）は430～440分付近です。 図6（残差プロット）で条件に合う点を探すと、 ・残差がマイナス（0より下） ・横軸（推定される睡眠時間）が対応する位置（※学業時間430分付近に対応する推定値） にあるのは、点「1」です。 正解は「1」です。 P県に対応する点（図6の点1）の縦軸（残差の変換値）の値を確認します。 点1は -1.5 と -2.0 の間にあり、およそ -1.8 程度です。 外れ値の基準は「絶対値が2以上」ですので、|-1.8| = 1.8 は 2未満となり、外れ値には該当しません。