共通テスト 情報I 対策問題集アプリ 第3問(共通テスト 試作問題-共通テスト 試作問題)

　当サイト・webアプリケーション・ページは、2025 年度大学入学共通テストから新教科として導入された「情報1」 の学習サイトです。
　現役ソフトウェアエンジニアと受験生向け塾講師の両経験を持つ運営主が、問題の作成からアプリの運営・開発まで一貫して行なっています。
　このページは問題一覧です。全ての問題を確認することで、情報1試験のインプット対策ができます。 　$ 問題タイトル：第3問問題カテゴリ：共通テスト 試作問題問題文：次の生徒（S）と先生（T）の会話文を読み、問い（問1～3）に答えよ。 S：この前、お客さんが460円の商品を買うのに、510円を払って、釣り銭50円を受け取っていたのを見て、授業で勉強したプログラミングで、そんな「上手な払い方」を計算するプログラムを作ってみたいと思いました。 T：いいですね。まず、「上手な払い方」とは何かを考える必要がありますね。ここでは、客が支払う枚数と釣り銭を受け取る枚数の合計を最小にする払い方を考えてみませんか？ （中略：100円以下の買い物とし、使う硬貨は1円、5円、10円、50円、100円玉のみとする） 【関数の説明】 枚数(金額)…引数として「金額」が与えられ、ちょうどその金額となる硬貨の組合せの中で、枚数が最小となる硬貨枚数が戻り値となる関数。 例：8円は「5円玉が1枚と1円玉が3枚」の組合せで最小の硬貨枚数になるので、枚数(8)の値は4となる。解説文：正解は「6」です。 46円を支払うための最小枚数を考えます。 最も効率的な組み合わせは、「10円玉×4枚、5円玉×1枚、1円玉×1枚」です。 枚数の合計は 4 + 1 + 1 = 6 枚となります。 正解は「0」です。 「客と店の間で交換される硬貨枚数の合計」を計算します。 ・客が支払う枚数：51円分の硬貨枚数 → 枚数(51) ・店から受け取る枚数：5円分の硬貨枚数 → 枚数(5) これらを合計するため、式は 枚数(51) + 枚数(5) となります。 正解は「2」です。 商品の価格 x 円に対し、釣り銭が y 円になるように支払う場合、支払う金額は x + y 円となります。 したがって、客が支払う硬貨の枚数は 枚数(x + y) となります。 正解は「1」です。 釣り銭として受け取る金額は y 円です。 したがって、受け取る硬貨の枚数は 枚数(y) となります。 全体として、交換枚数の合計は 枚数(x + y) + 枚数(y) で計算できます。 正解は「2」です。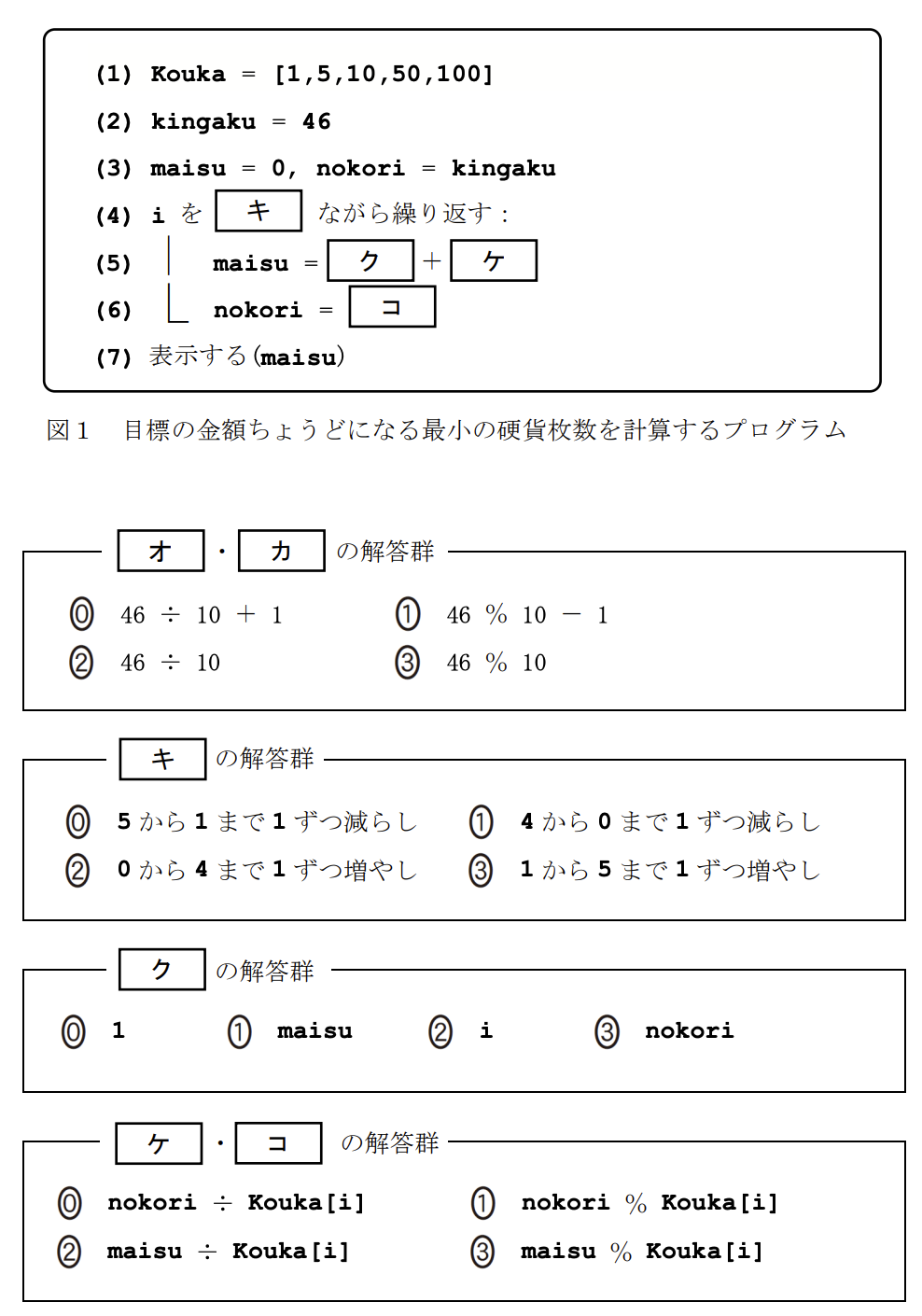 46円に対して10円玉が何枚使えるかを計算するには、整数の割り算（商）を用います。 46 ÷ 10 = 4（余り6）なので、4枚使えます。 プログラムでは整数除算を表す 46 ÷ 10 が適切です。 正解は「3」です。 46円を10円玉で支払った後の残金を計算するには、割り算の余りを用います。 46 ÷ 10 = 4 余り 6 なので、残金は6円です。 プログラムでは剰余演算子 % を使い、46 % 10 と表します。 正解は「1」です。 配列 Kouka には [1, 5, 10, 50, 100] が格納されており、インデックス（添字）は0から4に対応します（Kouka[4] が100円）。 先生のアドバイス「高額の硬貨から使うように」に従うため、インデックスの大きい方（4）から小さい方（0）へループさせる必要があります。 したがって、「4から0まで1ずつ減らし」が正解です。 正解は「1」です。 変数 maisu は、それまでに使った硬貨の枚数の合計を保持する変数です。 新たに計算した硬貨の枚数（[ケ]）を現在の合計に加算して更新する必要があるため、 maisu = maisu + ... の形になります。 正解は「0」です。 現在の残金 nokori に対して、硬貨 Kouka[i] が何枚使えるかを計算します。 これは [オ] と同様の処理なので、nokori ÷ Kouka[i]（整数除算）となります。 正解は「1」です。 硬貨を使った後の新しい残金を計算します。 これは [カ] と同様の処理なので、nokori % Kouka[i]（剰余）となります。 正解は「3」です。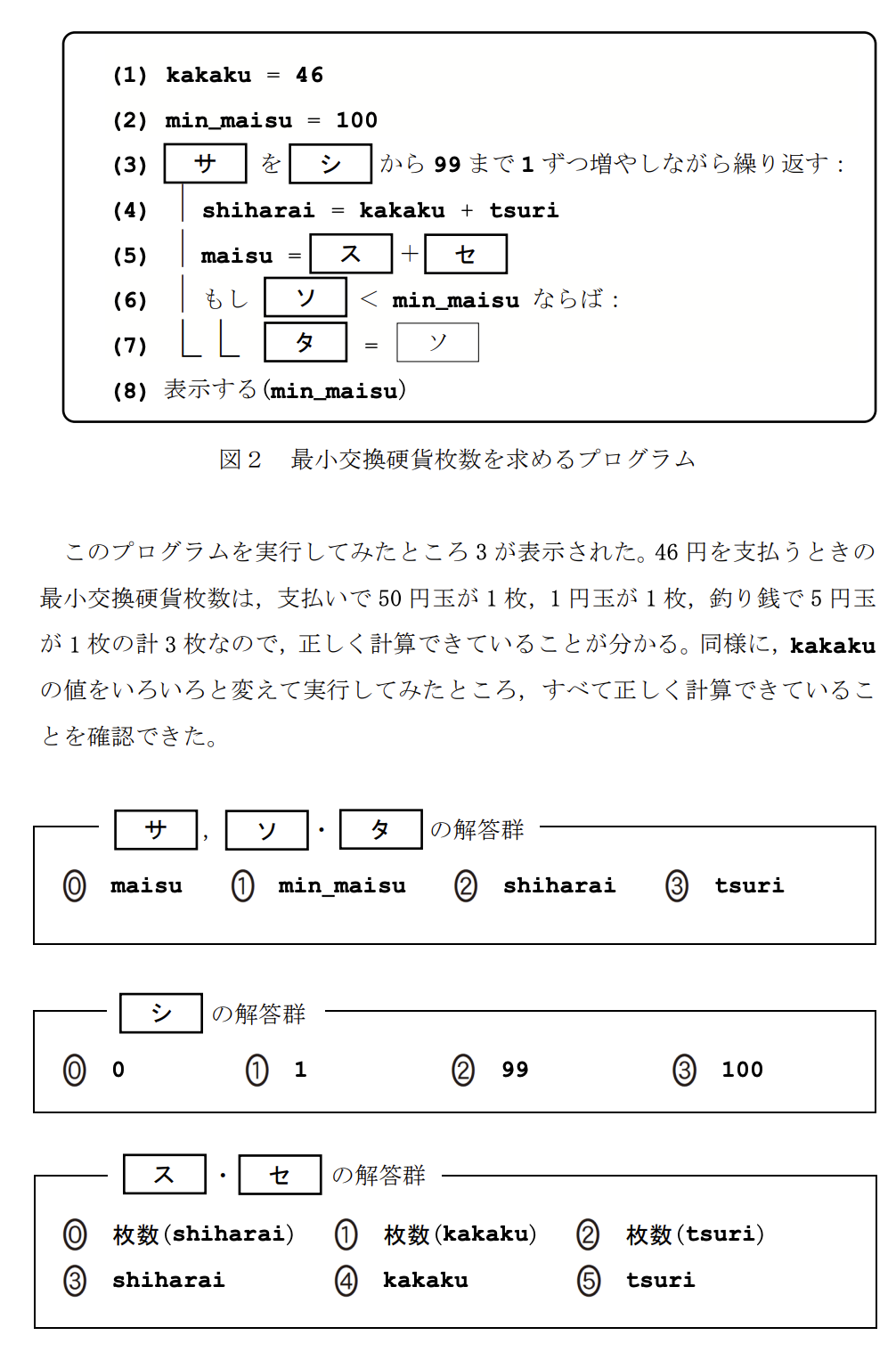 問題文に「釣り銭無しの場合も含め、99円までのすべての釣り銭に対し…」とあります。 変化させていく変数は「釣り銭」なので、tsuri が適切です。 正解は「0」です。 「釣り銭無し」とは「釣り銭が0円」であることを意味します。 0円から99円まで調べるため、開始値は「0」となります。 正解は「0」と「2」です。 交換する硬貨の合計枚数 maisu を計算します。 問1で導いた式 枚数(x + y) + 枚数(y) に当てはめます。 ・x + y（支払額）は変数 shiharai（4行目で計算済み） ・y（釣り銭）は変数 tsuri したがって、枚数(shiharai) と 枚数(tsuri) を足し合わせます。 正解は「0」です。 最小値を更新する条件判定です。 「これまでの最小値（min_maisu）」よりも「今回の計算結果（maisu）」が小さい場合に更新します。 したがって、条件式は maisu < min_maisu となります。 正解は「1」です。 条件を満たした場合、より小さい値である maisu を、最小値を記録する変数 min_maisu に代入（更新）します。 したがって、min_maisu = maisu となります。