共通テスト 情報I 対策問題集アプリ 第2問 B(共通テスト 試作問題-共通テスト 試作問題)

　当サイト・webアプリケーション・ページは、2025 年度大学入学共通テストから新教科として導入された「情報1」 の学習サイトです。
　現役ソフトウェアエンジニアと受験生向け塾講師の両経験を持つ運営主が、問題の作成からアプリの運営・開発まで一貫して行なっています。
　このページは問題一覧です。全ての問題を確認することで、情報1試験のインプット対策ができます。 　$ 問題タイトル：第2問 B問題カテゴリ：共通テスト 試作問題問題文：次の文章を読み、後の問い（問1～3）に答えよ。 Mさんのクラスでは、文化祭の期間中2日間の日程でクレープを販売することにした。1日目は客を待たせることが多かったため、調理手順を見直すなどの改善をした場合に待ち状況がどう変化するか、シミュレーションを行うことにした。なお、店では同時に一人の客しか対応できず、注文は前の客に商品を渡してから聞くものとする（1人あたりの対応時間は約4分）。 問1 Mさんは1日目の記録から「到着間隔」の分布を調べ（表1）、それに基づいた乱数を用いてシミュレーションを行った（表2）。 （表1：到着間隔と累積相対度数、表2：生成された乱数と到着間隔の対応表、図1：シミュレーション結果のタイムチャート）解説文：正解は「8」です。 表2の10人目の「生成させた乱数」は **0.95** です。 表1の「累積相対度数」を確認すると、 ・0.94 までが「7分」 ・0.96 までが「8分」 となっています。 乱数 0.95 は $0.94 < 0.95 \leqq 0.96$ の範囲に含まれるため、対応する階級値は「8分」となります。 正解は「4」です。 図1のシミュレーション結果（タイムチャート）を作成・補完して確認します。 前の客の対応終了を待って次の対応が始まるため、到着間隔が短いと待ち行列が発生します。 時間軸の **19分～20分** の時点を確認すると、6人目、7人目、8人目、9人目が「到着済み」かつ「対応未完了（または未開始）」の状態となり、待ち人数が最大で「4人」となります。 正解は「1」です。 最も待ち時間が長いのは9人目で、待ち時間は「13分」です。 空欄 [サ] はその10の位を表すため、「1」が正解となります。 正解は「3」です。 最も待ち時間が長いのは9人目で、待ち時間は「13分」です。 空欄 [シ] はその1の位を表すため、「3」が正解となります。 （計算詳細：9人目の到着は開始19分後、対応開始は前の客が終わる32分後。$32 - 19 = 13$分） 正解は「1」です。 シミュレーション結果（図2）から「読み取れない（誤っている）もの」を選びます。 左上の「来客人数10人」のグラフを見ると、最大待ち人数が「6人」の頻度が存在します。 来客人数10人の半数は5人ですが、6人はそれより多いため、「最大待ち人数の分布は、来客人数の半数以下に収まっている」という記述は正しくありません。 正解は「0」です。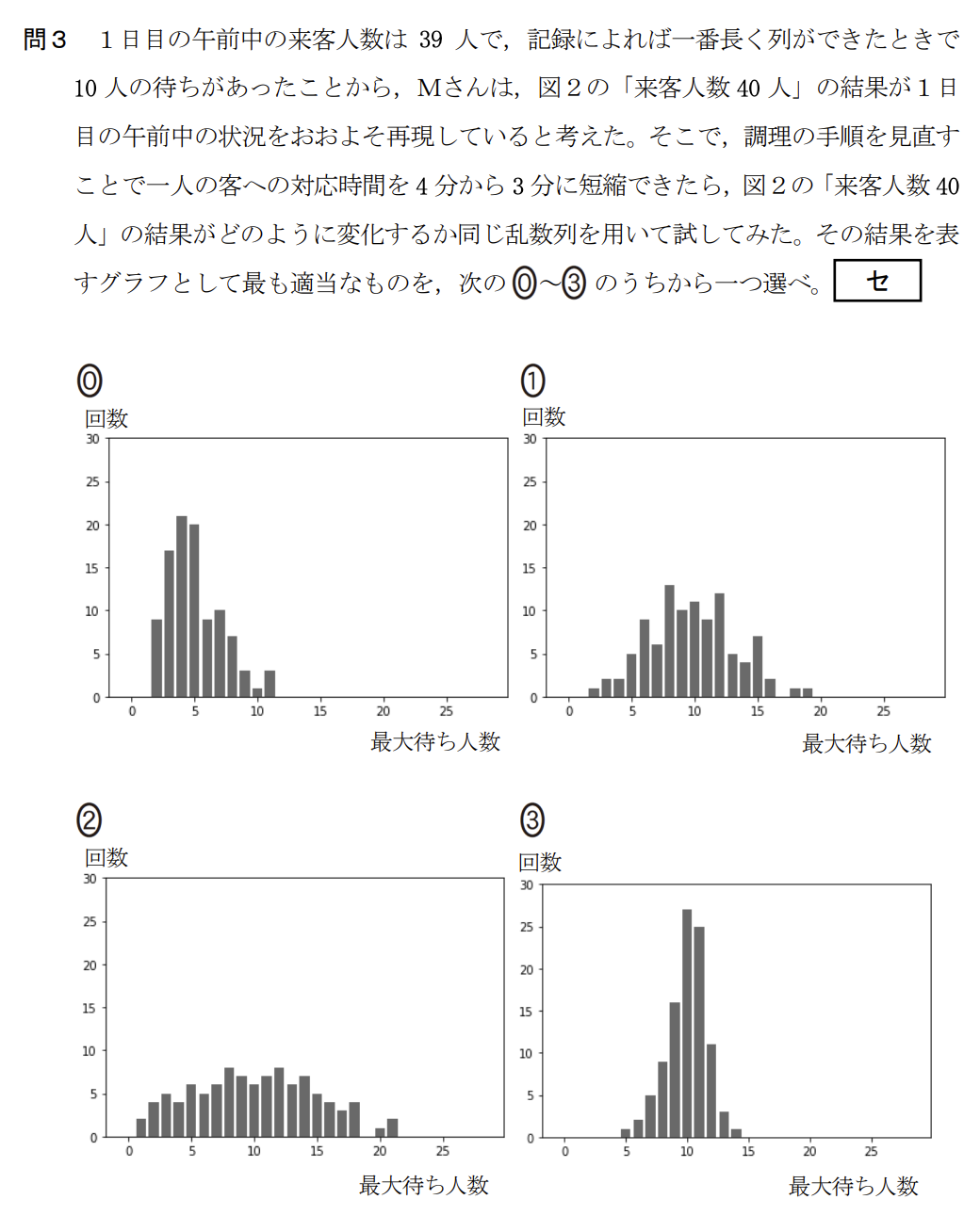 対応時間を4分から3分に短縮した場合、客の流れがスムーズになり、待ち人数は減少すると予測できます。 グラフの形状としては、元の「来客人数40人」のグラフ（ピークが10人付近）よりも、全体的に左側（人数の少ない方）へシフトするはずです。 選択肢のグラフを確認すると、「0」のグラフのみがピークが5人付近に移動しており、待ち人数が減少している状況を適切に表しています。